Risk Analysis Explained

Published: 2009-02-28
Last updated: 2022-03-20

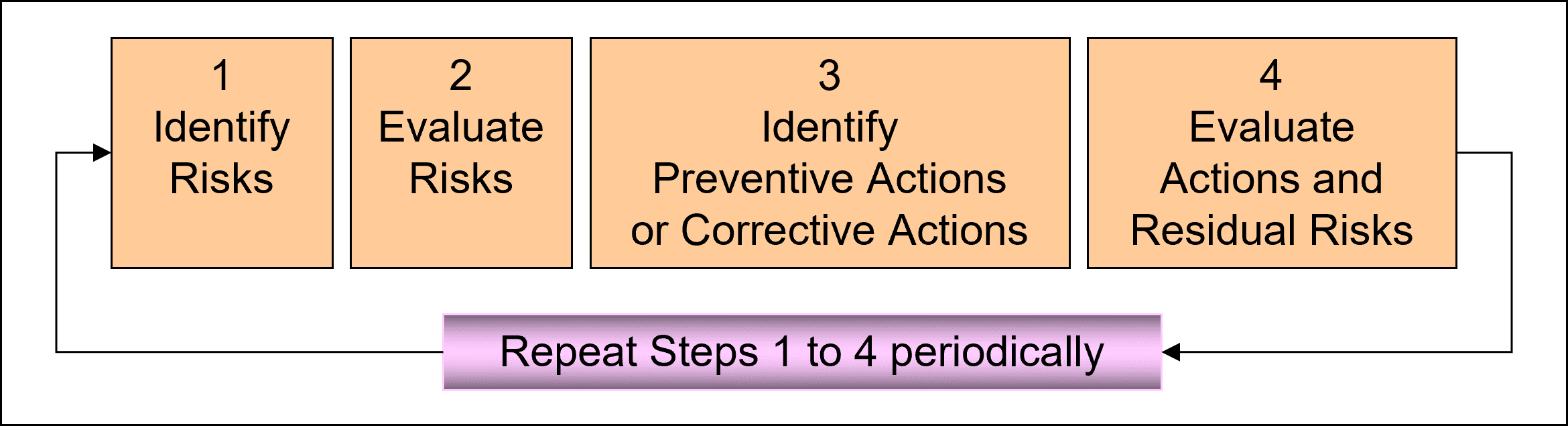
Risk analysis is one of the most powerful project management tools we have. In sub-section Risk Management, we introduced the risk management process.

Risk Management Process

Here, we focus on what we can do in order to analyze risks and their impacts.

In sub-section Risk Management, we introduce the definition of the term risk:

Risk = probability (event with negative impact may happen).

For a given work package, identifying risks is about asking the question: what can happen that makes the achievement of that work package's results impossible or more difficult than usual? This leads to a list of risk events.

In the next step, we evaluate each risk event: what is the probability that it happens and what is its impact? This evaluation we call risk analysis.

Risk Analysis: Just Guess Work?

In case data from earlier projects with similar work packages, and thus, similar risk events, are not available, we end up with simply doing guess work. Like in effort estimation, we can ask experienced experts who give us their best guess on probability (= risk) and impact of such an event. In order to make our guess work a little bit more reliable, we ask the experts for their best guess, normal guess, and worst guess in terms of both, probability and impact.

Example

Work package: Delivery of 200 photovoltaic panels, 224 Watt and USD 1,800.-- each. One event could be: delay of that delivery by 4 weeks. Our experts give us their estimates of probabilities

and impact:

How can we use these estimates for risk analysis without making it too complicated (by combining 3 probability figures with 3 impact figures we would end up with 9 different values to follow up)?

As in the Delphi Method of effort estimation, we could calculate for probability

p = (p_best + 4 • p_normal + p_worst) / 6 =
= (5 + 40 + 20) / 6 =
= 11%

and similarly for impact

i = (i_best + 4 • i_normal + i_worst) / 6 =
= (3,000 + 120,000 + 90,000) / 6 =
= 35,500.-- USD

After this "risk analysis", which is actually guess work, we continue with the next step of the risk management process which we describe more detailed in sub-section Risk Management.

Risk Analysis: the Next Level

Now let us assume that our organization supports a knowledge management process with a project management information system in which we collect data about risks of earlier projects.

For certain work packages that are similar from project to project, we have data available. With a little bit of mathematical statistics we can use those data to replace, or at least back up, our guess work in a new project by some simple calculations.

Underlying assumption of the approach we describe below is: we have done a certain work package 50 times already, in 50 earlier projects; this is not unusual for most of our organizations. Now, we apply some mathematical statistics to those data.

Of course, it might be the case that those 50 work packages were not exactly the same. In our example above, delivery of a number of photovoltaic panels, it makes a difference if we had to deliver within our own country or across borders, if the panels had to be state of the art or off-the-shelf units, if the delivery went into a remote area or nearby a town, etc. So, we refer to those work packages that had to be carried out under similar or comparable conditions. Then, we will identify similar or comparable risk events.

For these risk events, we continue with risk analysis as follows. In our risk data base, we find actual data about how often a certain risk event happened and what impact it really had. Then, we can calculate:

In our further risk analysis, we now can take values for probability and impact out of the intervals

from p_mean – p_SD to p_mean + p_SD
and
from i_mean – i_SD to i_mean + i_SD

or maybe, with 2 • p_SD or even 3 • p_SD, and 2 • i_SD or even 3 • i_SD, respectively, depending on how far we want to be on the safe side.

Example

In our example above, we find 20 similar work packages from earlier projects in our data base. The values for probability and impact are:

p_mean = 9%
p_SD = 1%

i_mean = USD 28,000.--
i_SD = USD 3,000.-

For the new work package under risk analysis, we can choose values for

p, from 8% to 10%
and
i, from USD 25,000.-- to USD 31,000.--

under the condition that + or – 1 single standard deviation gives us enough safety.

Remarks

(1) Quantity of data: It is clear that this method of risk analysis only works where we have a certain minimum of data from earlier projects. A number of 10 is minimum requirement, the more the better. Therefore, project managers and team members must be motivated to contribute all the actual results of their projects.

(2) Quality of data: It is absolutely essential that we refer only to work packages that were carried out under the same or comparable conditions. This accounts again for a high level of motivation of project managers and team members to fill the risk data base with all available details, including work package requirements and specifications, assumptions, interpretation of contract wordings, etc.

35+ templates, tools, and checklists in one set

To save you time in your daily work as a project manager, I packaged more than 35 project management templates, tools, and checklists into one zip file.

• You un-zip it, and you get all items in formats you can edit to your requirements.
• They strictly contain only standard functionality and no macros or other code.
• You are allowed to use your logo.

for only
or click here for more info.